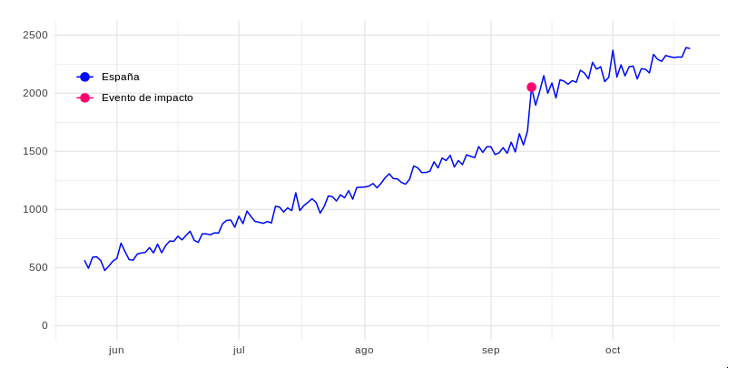
 El punto fucsia representa el número de visitantes únicos el día que, por ejemplo, arrancó una campaña de marketing determinada, a la cual nos referiremos a ella como evento de impacto. Supongamos que tenemos nuestra misma web en otros países como Italia y Portugal (grupos de control), donde el evento de impacto no ha ocurrido:
El punto fucsia representa el número de visitantes únicos el día que, por ejemplo, arrancó una campaña de marketing determinada, a la cual nos referiremos a ella como evento de impacto. Supongamos que tenemos nuestra misma web en otros países como Italia y Portugal (grupos de control), donde el evento de impacto no ha ocurrido: 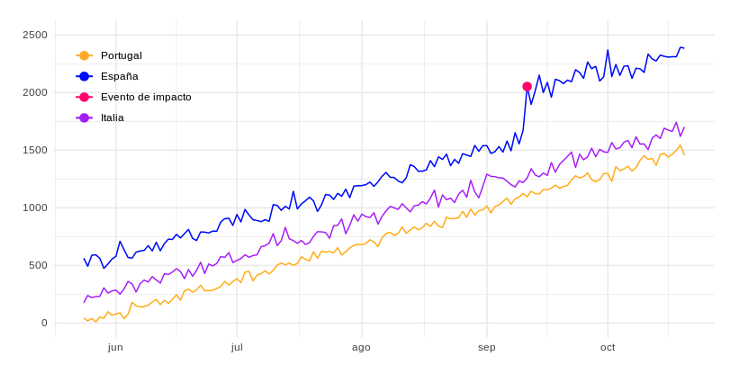 Con el algoritmo de Causal Impact podríamos crear un modelo basado en los datos de visitantes únicos de estos países para proyectar los valores esperados en el mismo período de tiempo en España. Actuando como serie base e indicando el número de visitantes únicos que hubiéramos esperado en España, en caso de que no se hubiese realizado la campaña. Se muestra como la línea morada a continuación:
Con el algoritmo de Causal Impact podríamos crear un modelo basado en los datos de visitantes únicos de estos países para proyectar los valores esperados en el mismo período de tiempo en España. Actuando como serie base e indicando el número de visitantes únicos que hubiéramos esperado en España, en caso de que no se hubiese realizado la campaña. Se muestra como la línea morada a continuación: 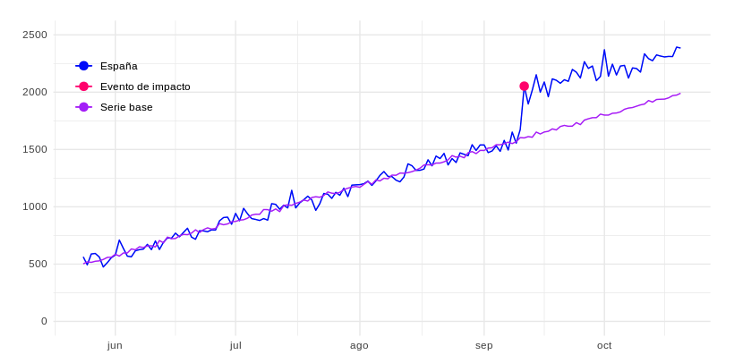 Una vez que obtenemos esta serie base, podemos calcular las diferencias entre las dos series de tiempo, los valores reales de España y los valores estimados si no se hubiese producido el evento de impacto. Y así, considerar la diferencia como el impacto real del evento, tal y como se representa a través de la línea morada en la siguiente figura:
Una vez que obtenemos esta serie base, podemos calcular las diferencias entre las dos series de tiempo, los valores reales de España y los valores estimados si no se hubiese producido el evento de impacto. Y así, considerar la diferencia como el impacto real del evento, tal y como se representa a través de la línea morada en la siguiente figura: 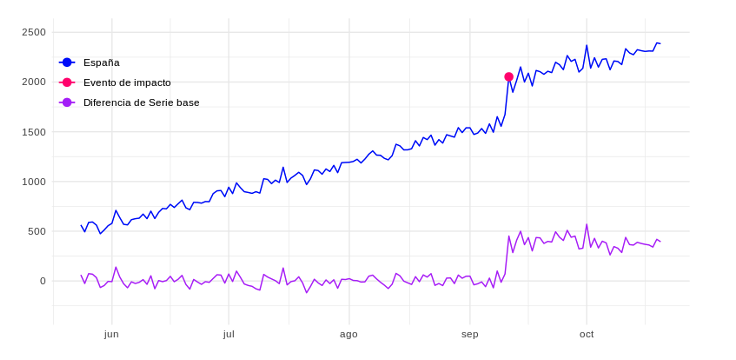 O por otra parte, acumular la serie para poder ver el impacto total hasta cualquier fecha dada. La línea fucsia a continuación representa esto:
O por otra parte, acumular la serie para poder ver el impacto total hasta cualquier fecha dada. La línea fucsia a continuación representa esto: 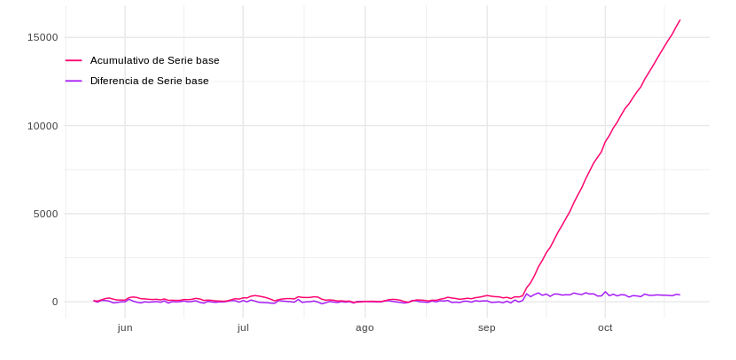 De esta manera, podemos medir el ROI (retorno de la inversión) de dicha campaña de una forma mucho más justa, incluso cuando no estamos seguros de si el evento fue la única fuente de impacto. El algoritmo de Causal Impact ayuda a obtener esta información rápidamente para poder ajustar cualquier acción de manera oportuna con confianza.
De esta manera, podemos medir el ROI (retorno de la inversión) de dicha campaña de una forma mucho más justa, incluso cuando no estamos seguros de si el evento fue la única fuente de impacto. El algoritmo de Causal Impact ayuda a obtener esta información rápidamente para poder ajustar cualquier acción de manera oportuna con confianza.
El algoritmo Causal Impact
La idea principal del algoritmo es construir una serie temporal bayesiana basada en múltiples grupos de control (en el ejemplo anterior, Italia y Portugal), y ajustar las diferencias de tamaño entre los grupos de control y el grupo de test (España) para obtener una serie base sintética. Los grupos de control son aquellos en los que no tuvimos el evento de impacto. Por lo que no se esperan ver cambios en la serie producidos por dicho evento. El grupo de test es aquel donde se produjo el evento de impacto, y esperamos que este haya producido algún cambio en la serie temporal.
¿Qué es la serie base sintética?
Básicamente, se trata de una serie de valores que hubiéramos esperado en el grupo de test sin el evento de impacto. A diferencia de otros algoritmos basados en series de tiempo, donde las predicciones se hacen con los valores pasados del grupo de test, este algoritmo construye el modelo a través de los grupos de control para un tiempo posterior al evento de impacto. Esto significa que los grupos de control, o la combinación entre ellos, deben tener correlación con el grupo de test para que el algoritmo realice predicciones de confianza.
¿Cómo elegir grupos de control correlacionados?
El algoritmo Causal Impact selecciona de forma automática el grupo o grupos de control más correlacionados mediante la técnica Bayesiana de selección de variables spike-and-slab. Pero la técnica que propuso Kim Larsen complementa el algoritmo de Causal Impact para obtener los grupos más correlacionados. Esta técnicas es conocida como Dynamic time warping (DTW).
DTW
Obtener la correlación sin más, entre dos series de tiempo, ignora un fenómeno que se produce habitualmente en las series, que es el desplazamiento temporal: 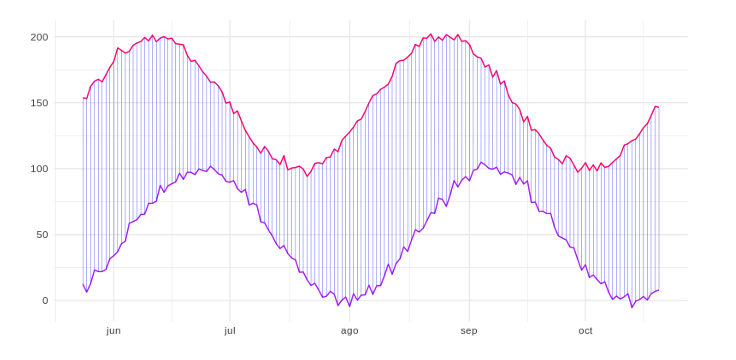 Las dos series anteriores no tienen las modas posicionadas en el mismo momento, pero con solo observarlas se puede ver que hay una alta “correlación” entre ellas. Los máximos y mínimos de la línea morada vienen un poco más tarde que los de la línea fucsia. Por lo tanto, calcular las distancias uno a uno según el eje temporal ignoraría el desplazamiento y podría etiquetar estas dos series como diferentes en lugar de similares. La técnica DTW permite hacer un mapeo one-to-many, calculando las distancias de una serie de tiempo con respecto a otra, teniendo en cuenta los posibles desplazamientos temporales que podría haber entre ambas (correlación cruzada). Tal y como se muestra en la siguiente figura:
Las dos series anteriores no tienen las modas posicionadas en el mismo momento, pero con solo observarlas se puede ver que hay una alta “correlación” entre ellas. Los máximos y mínimos de la línea morada vienen un poco más tarde que los de la línea fucsia. Por lo tanto, calcular las distancias uno a uno según el eje temporal ignoraría el desplazamiento y podría etiquetar estas dos series como diferentes en lugar de similares. La técnica DTW permite hacer un mapeo one-to-many, calculando las distancias de una serie de tiempo con respecto a otra, teniendo en cuenta los posibles desplazamientos temporales que podría haber entre ambas (correlación cruzada). Tal y como se muestra en la siguiente figura: 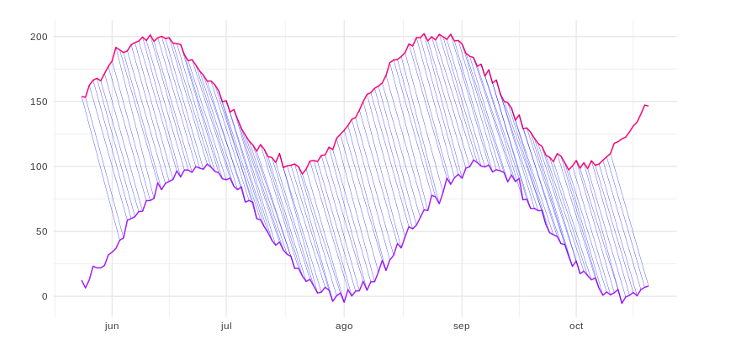 Al emplear este algoritmo podemos calcular la distancia entre estas dos líneas aunque exista desplazamiento temporal, y por lo tanto podemos considerar que estas son más similares o “correlacionadas” de lo que podrían haber sido sin él. Otros casos que corrige DTW es determinar que existe correlación entre dos series aunque una esté contraída o dilatada con respecto a la otra. Básicamente podemos usar el algoritmo DTW para encontrar los grupos de control más similares al grupo de test y pasarlos al algoritmo de Causal Impact como predictores, ¡y luego dejar que el algoritmo haga su trabajo!
Al emplear este algoritmo podemos calcular la distancia entre estas dos líneas aunque exista desplazamiento temporal, y por lo tanto podemos considerar que estas son más similares o “correlacionadas” de lo que podrían haber sido sin él. Otros casos que corrige DTW es determinar que existe correlación entre dos series aunque una esté contraída o dilatada con respecto a la otra. Básicamente podemos usar el algoritmo DTW para encontrar los grupos de control más similares al grupo de test y pasarlos al algoritmo de Causal Impact como predictores, ¡y luego dejar que el algoritmo haga su trabajo!






 Configuración de cookies
Configuración de cookies