Cuando k-means es la solución
Supongamos que tenemos el siguiente dataset con 2 dimensiones. Por ejemplo, imaginemos que estas variables son el peso y la altura normalizadas (de 0 a 1) de un conjunto de personas: 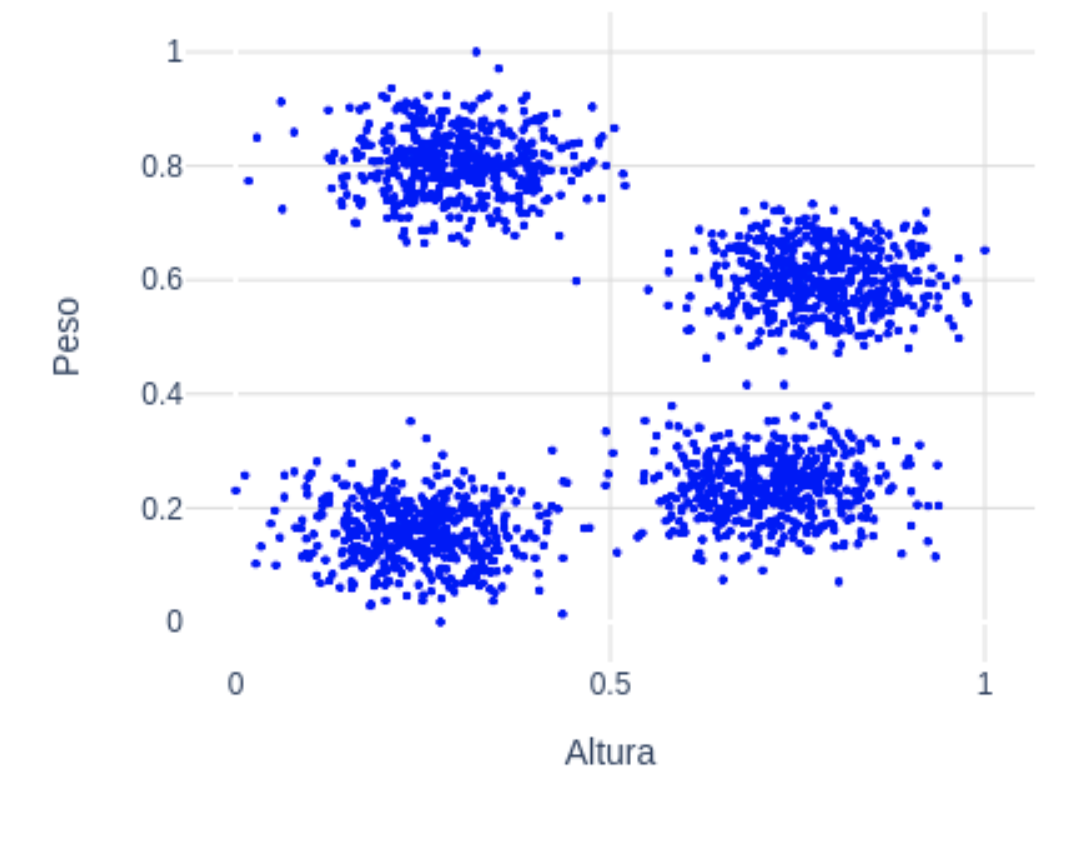 A simple vista se pueden diferenciar 4 grupos claramente. Esta información servirá de entrada para k-means: k=4. Una vez el algoritmo recibe el número de grupos deseado los pasos que sigue son sencillos:
A simple vista se pueden diferenciar 4 grupos claramente. Esta información servirá de entrada para k-means: k=4. Una vez el algoritmo recibe el número de grupos deseado los pasos que sigue son sencillos:
- Se inicializan k centroides aleatoriamente, en este caso k=4 centroides.
- Se clasifica cada punto del dataset calculando la distancia de cada punto a cada centroide. Cada punto pertenece al grupo cuyo centroide se encuentra más cercano.
- Con los grupos creados en el paso 2, se recalculan los centroides como la media de todos los puntos del grupo. De ahí el nombre k-means.
- Se repiten los pasos 2 y 3 hasta que los centroides ya no cambian demasiado por cada iteración.
Para más detalle así como una implementación simple en python, puedes consultar este artículo. Como vemos en la siguiente figura, k-means consigue segmentar el dataset tal y como lo esperábamos: 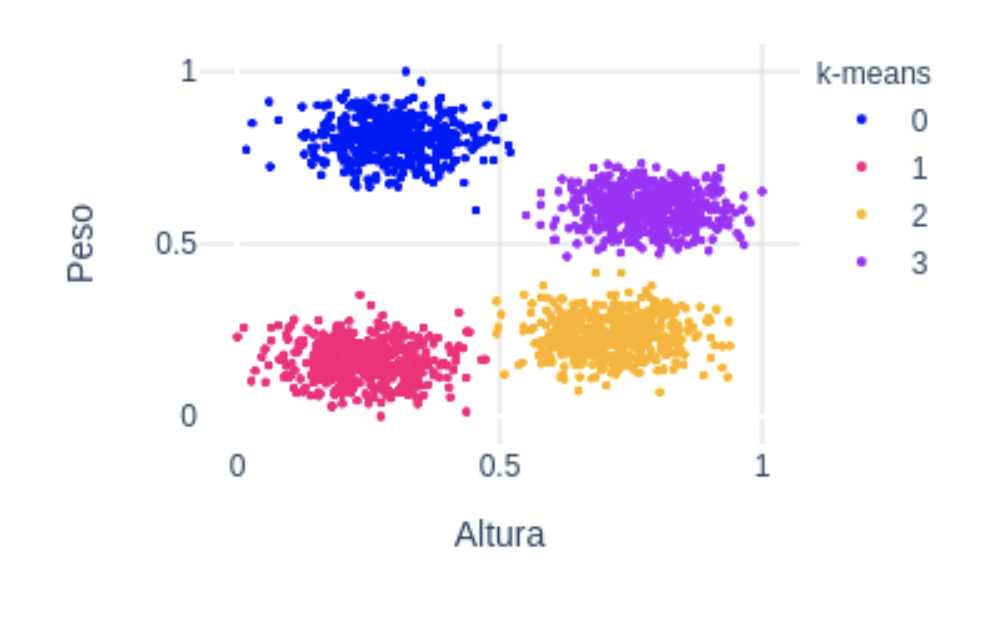
¿Es siempre k-means la opción más recomendable?
La respuesta es no. Hay tipos de datos en los que k-means, por su propia naturaleza, no funciona de la forma deseada. Como hemos visto, para que k-means tenga un funcionamiento adecuado los centroides, i.e. las medias de cada cluster, tienen que estar suficientemente alejados. Además, en el punto 3 del algoritmo k-means se recalculan los centroides calculando la media de cada grupo. Esto “fuerza” que los clusters tiendan a ser circulares por el hecho de que el centroide está justo en el centro del cluster. Pero, ¿qué pasaría si nuestros datos no son circulares, o si los centroides no están suficientemente alejados?
Gaussian Mixture Model (GMM)
Si los grupos que vemos a simple vista no son “circulares”, puede que k-means no sea la opción a utilizar. En el siguiente dataset vemos 3 grupos claramente diferenciables a simple vista. Estos tienen forma elíptica, no circular: 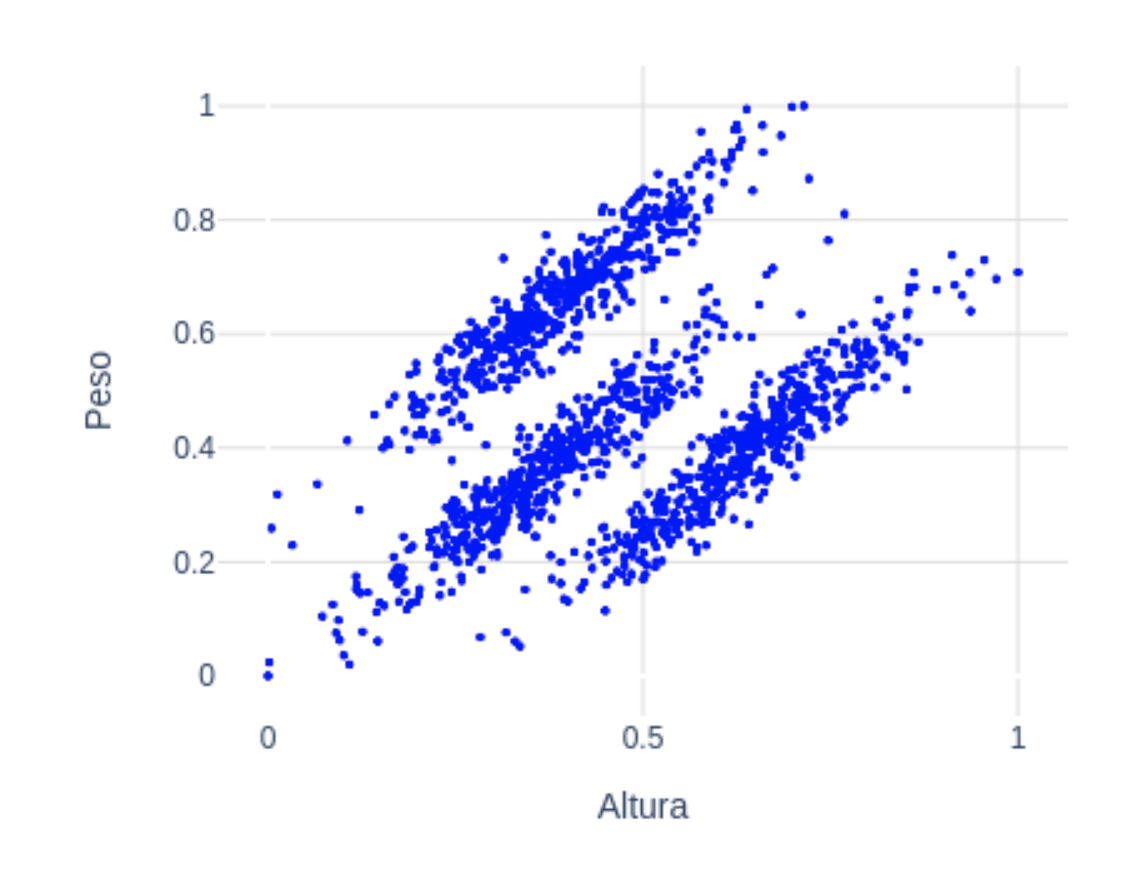 Para este tipo de datos, una buena opción podría ser Gaussian Mixture Models (GMM). Con este algoritmo asumimos que los puntos siguen una distribución Gaussiana. Esta asunción es menos restrictiva que suponer que son circulares como en el caso de k-means. De hecho, k-means es un caso especial de GMM donde la covarianza de cada cluster en todas las dimensiones tiende a 0. Con GMM, los clusters tienen 2 parámetros a optimizar: la media y la desviación típica. Con estos parámetros, en este ejemplo con 2 dimensiones, los clusters pueden adoptar cualquier forma elíptica. En este enlace tienes más detalle, así como una implementación simple en python.
Para este tipo de datos, una buena opción podría ser Gaussian Mixture Models (GMM). Con este algoritmo asumimos que los puntos siguen una distribución Gaussiana. Esta asunción es menos restrictiva que suponer que son circulares como en el caso de k-means. De hecho, k-means es un caso especial de GMM donde la covarianza de cada cluster en todas las dimensiones tiende a 0. Con GMM, los clusters tienen 2 parámetros a optimizar: la media y la desviación típica. Con estos parámetros, en este ejemplo con 2 dimensiones, los clusters pueden adoptar cualquier forma elíptica. En este enlace tienes más detalle, así como una implementación simple en python. 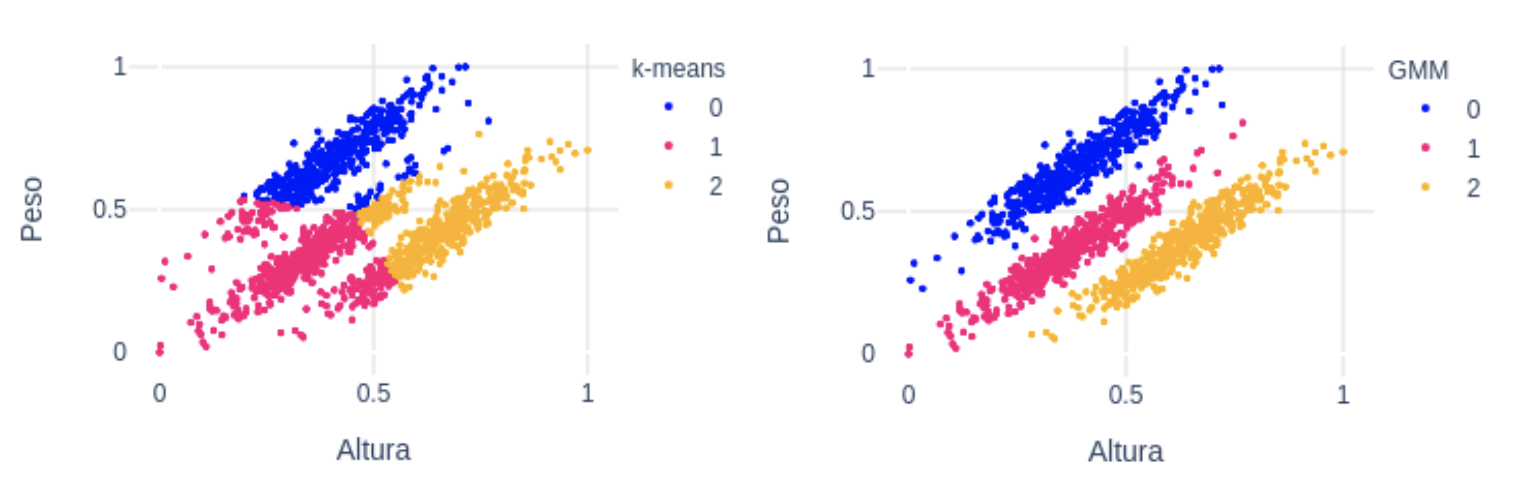 Como podemos ver en la figura de arriba, k-means (izquierda) en este caso no ha sido capaz de diferenciar bien los 3 grupos. En cambio, GMM (derecha) sí ha sido capaz de encontrarlos, gracias al parámetro de la desviación típica.
Como podemos ver en la figura de arriba, k-means (izquierda) en este caso no ha sido capaz de diferenciar bien los 3 grupos. En cambio, GMM (derecha) sí ha sido capaz de encontrarlos, gracias al parámetro de la desviación típica.
Density-Based Spatial Clustering of Applications with Noise (DBSCAN)
En un ejercicio de imaginación, supongamos ahora que nuestros datos con las variables altura y peso tienen esta pinta: 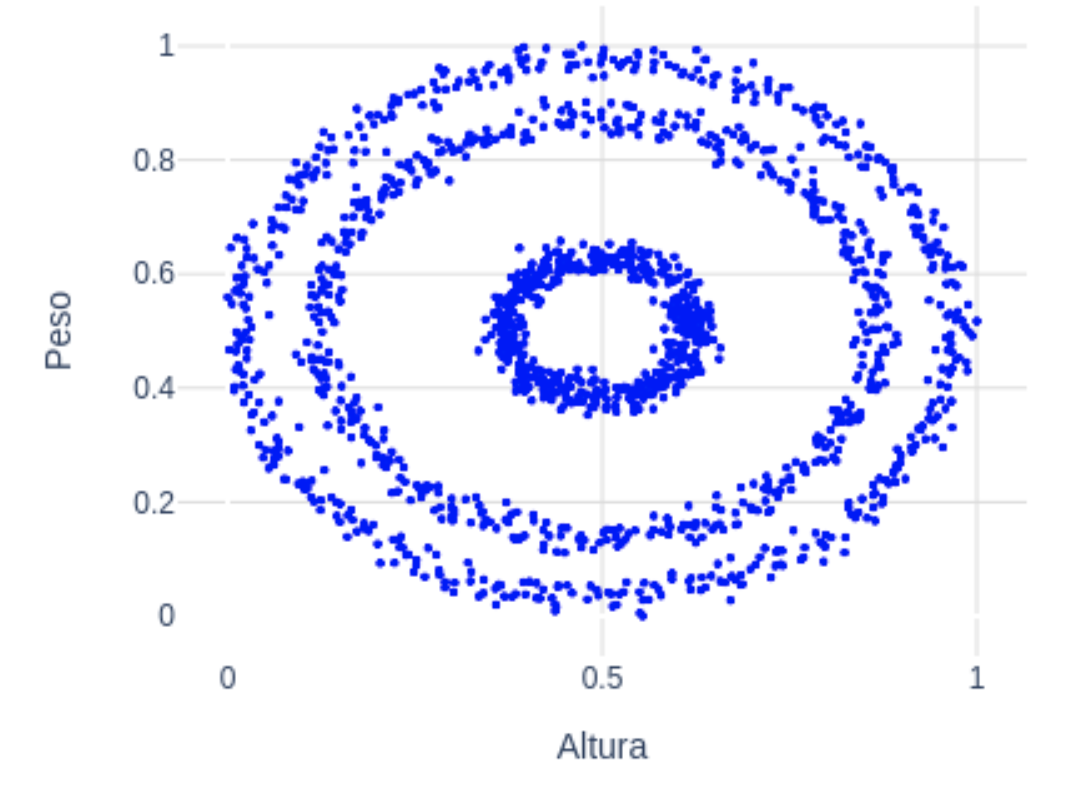 A simple vista es fácil distinguir 3 grupos, que se corresponden con los 3 anillos concéntricos que se observan. En este caso, ni k-means ni GMM van ser capaces de separar los 3 grupos dado que la media ideal de cada grupo se encontraría en el mismo punto: en el centro. En la siguiente figura, vemos precisamente cómo los clusters que devuelven k-means (izquierda) y GMM (derecha) no son válidos para estos datos:
A simple vista es fácil distinguir 3 grupos, que se corresponden con los 3 anillos concéntricos que se observan. En este caso, ni k-means ni GMM van ser capaces de separar los 3 grupos dado que la media ideal de cada grupo se encontraría en el mismo punto: en el centro. En la siguiente figura, vemos precisamente cómo los clusters que devuelven k-means (izquierda) y GMM (derecha) no son válidos para estos datos: 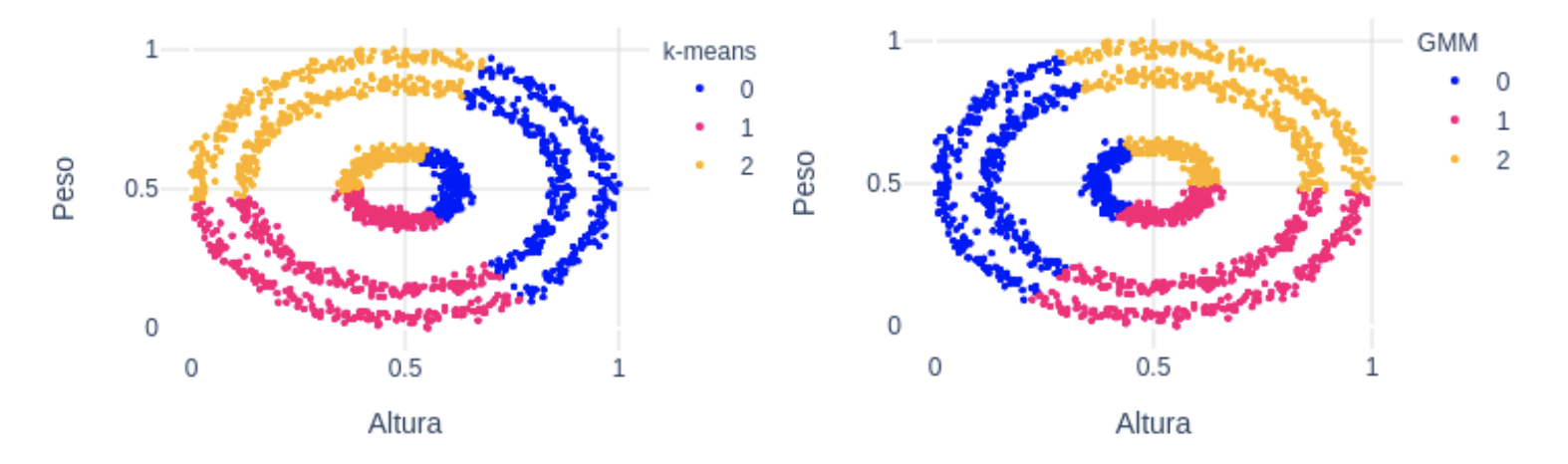 En este caso, utilizar el algoritmo Density-Based Spatial Clustering of Applications with Noise (DBSCAN) puede ser la opción correcta. Una característica de este algoritmo es que no necesita recibir el número de clusters como parámetro, sino que el propio algoritmo encuentra el número óptimo de clusters. El funcionamiento es sencillo:
En este caso, utilizar el algoritmo Density-Based Spatial Clustering of Applications with Noise (DBSCAN) puede ser la opción correcta. Una característica de este algoritmo es que no necesita recibir el número de clusters como parámetro, sino que el propio algoritmo encuentra el número óptimo de clusters. El funcionamiento es sencillo:
- Se recibe como parámetro , que es la distancia con la que vamos a trabajar y min_points.
- Se empieza con un punto cualquiera del dataset y se miran los puntos que están a distancia de este punto. Si el número de puntos encontrados es mayor que min_points, entonces el algoritmo empieza y consideramos al punto actual como el primer punto del nuevo cluster, si no, este punto se considera ruido.
- Todos los puntos que están a distancia del punto actual se unirán al cluster. Este proceso se repite para todos los puntos nuevos que se han añadido al cluster.
- Los pasos 2 y 3 se repiten hasta que todos los puntos del cluster han sido etiquetados.
- Cuando terminamos con el primer cluster, se elige aleatoriamente otro punto no visitado anteriormente y se repite el proceso hasta que todo el dataset ha sido etiquetado, ya sea como perteneciente a un cluster o como ruido.
Para más detalle con este algoritmo puedes consultar el siguiente artículo donde también se incluye una implementación sencilla en python. En la figura de abajo vemos cómo DBSCAN ha sido capaz de segmentar correctamente todos los puntos del dataset. 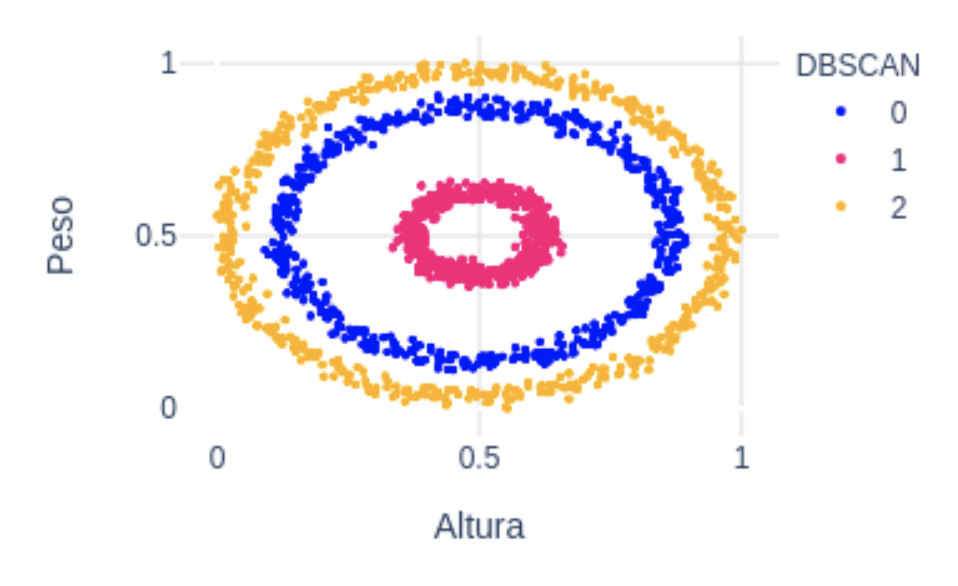
Cuando los datos son sparse
Finalmente, vamos a ver un tipo de datos diferente a los anteriores. Supongamos que tenemos un e-commerce donde vendemos productos de 30 categorías diferentes: moda, electrónica, libros, hogar, etc. Tenemos datos de nuestros usuarios (20k usuarios) que nos indican el número de compras ponderados que han realizado de cada categoría. Aquí podemos ver un extracto de estos datos: 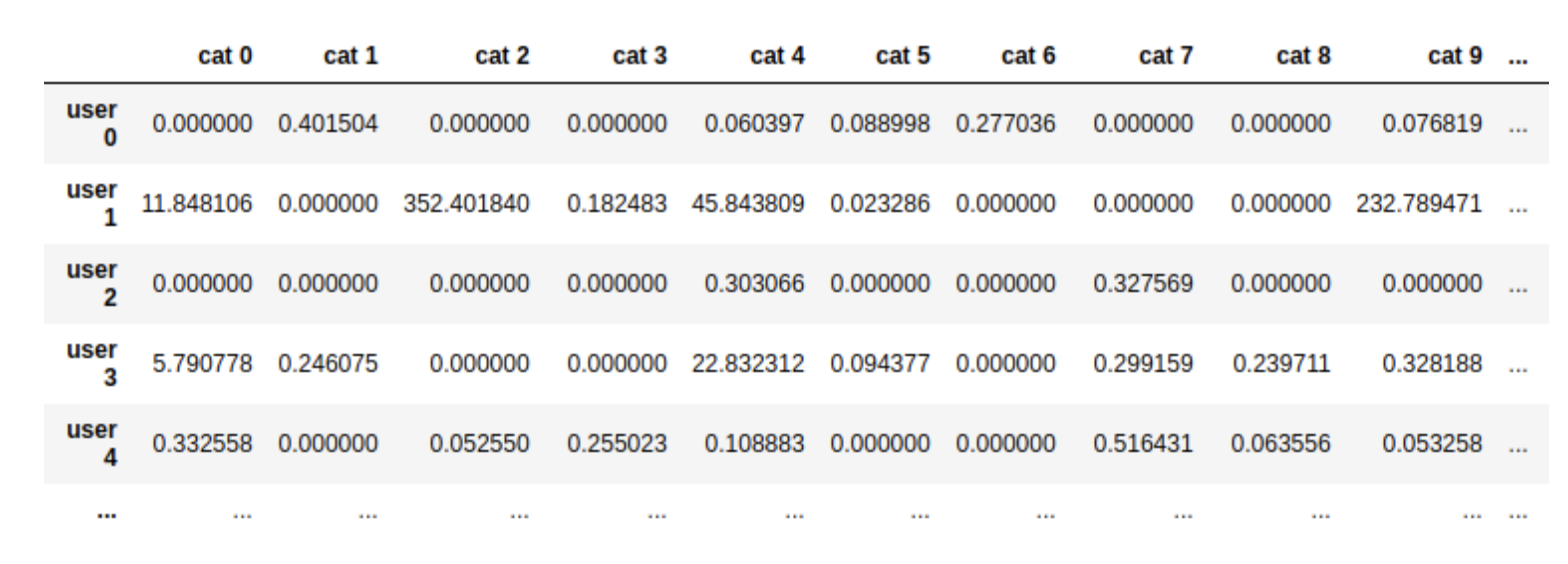 Como vemos, los datos son sparse, es decir, hay muchos ceros. Esto es debido a que, por lo general, los usuarios realizan compras de unas pocas categorías, pero no de todas. El objetivo de aplicar clustering en estos datos es conseguir obtener grupos de usuarios en base a sus compras. Idealmente, obtendremos grupos de usuarios que compran varias categorías de productos y por lo tanto tienen un comportamiento similar en nuestra web. Si utilizamos k-means para clusterizar a los usuarios ocurre lo siguiente:
Como vemos, los datos son sparse, es decir, hay muchos ceros. Esto es debido a que, por lo general, los usuarios realizan compras de unas pocas categorías, pero no de todas. El objetivo de aplicar clustering en estos datos es conseguir obtener grupos de usuarios en base a sus compras. Idealmente, obtendremos grupos de usuarios que compran varias categorías de productos y por lo tanto tienen un comportamiento similar en nuestra web. Si utilizamos k-means para clusterizar a los usuarios ocurre lo siguiente: 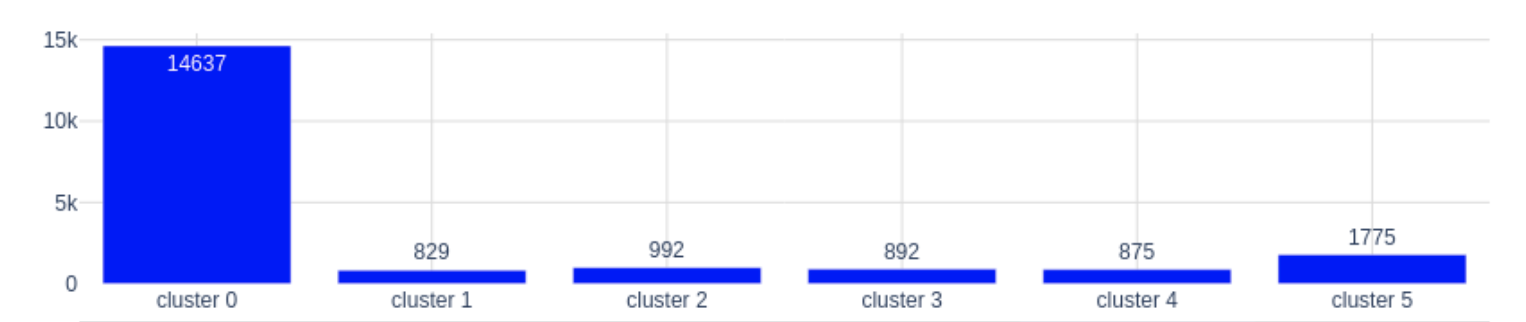
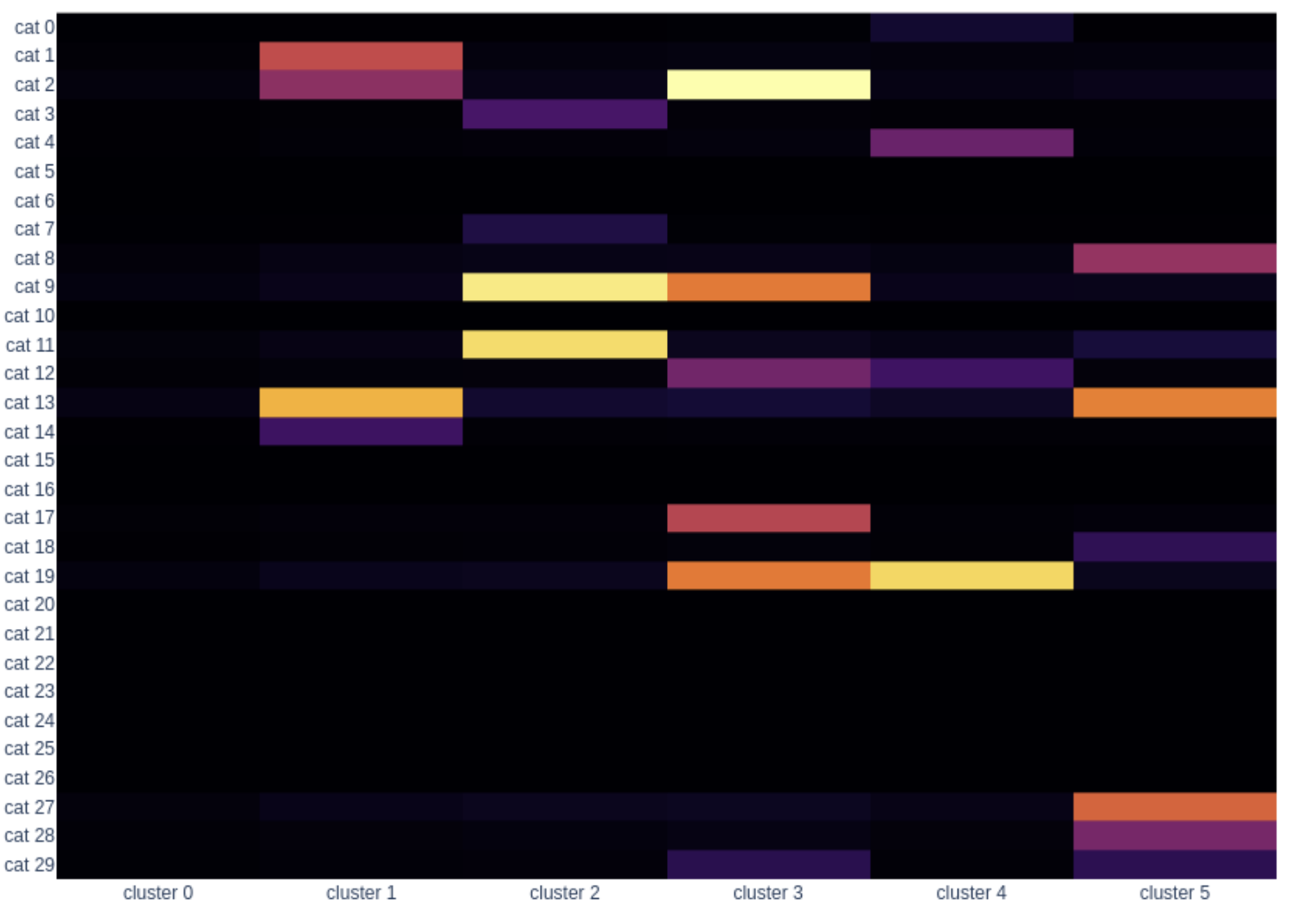 En la figura de arriba vemos por un lado el tamaño de cada cluster, y debajo, vemos cómo son los centroides. Cuanto más intenso es el color, más importancia tiene esa categoría en ese cluster. Lo que ha identificado k-means es que hay un grupo muy numeroso (cluster 0) que casi no compra en comparación con los otros. Los demás, aunque estén formados por muy pocos usuarios sí tienen bastantes compras y se han agrupado en base a las diferentes categorías. Esto de cara al negocio puede que no sea muy útil ya que el objetivo es encontrar patrones de comportamiento en cuanto a las categorías para que los grupos se puedan activar de alguna manera y con k-means estamos descartando a 14k usuarios al meterlos en el grupo de usuarios que compran poco en vez de agruparlos también según las categorías que compran.
En la figura de arriba vemos por un lado el tamaño de cada cluster, y debajo, vemos cómo son los centroides. Cuanto más intenso es el color, más importancia tiene esa categoría en ese cluster. Lo que ha identificado k-means es que hay un grupo muy numeroso (cluster 0) que casi no compra en comparación con los otros. Los demás, aunque estén formados por muy pocos usuarios sí tienen bastantes compras y se han agrupado en base a las diferentes categorías. Esto de cara al negocio puede que no sea muy útil ya que el objetivo es encontrar patrones de comportamiento en cuanto a las categorías para que los grupos se puedan activar de alguna manera y con k-means estamos descartando a 14k usuarios al meterlos en el grupo de usuarios que compran poco en vez de agruparlos también según las categorías que compran.
Non-negative Matrix Factorization (NMF)
Non-negative Matrix Factorization (NMF) es una técnica que tiene una propiedad inherente para clusterizar y es utilizada ampliamente para ello, especialmente cuando los datos de entrada son sparse. La idea de esta técnica es tratar de aproximar una matriz V mediante la multiplicación de dos matrices no negativas, W y H:
V=WH
Donde V es nuestro dataset transpuesto, que tiene dimensiones f x n, donde f es el número de categorías y n es el número de usuarios. Por lo tanto, la matriz resultante W tiene dimensiones f x t, y la matriz resultante H, t x n, siendo t el número de clusters recibido como entrada del algoritmo. Las columnas de la matriz resultante WH son una combinación lineal de los t clusters representados como las t columnas de W. Esto es importante ya que es la base del NMF: se asume que cada columna en V está construida a partir de un número pequeño (t) de features desconocidas y lo que se consigue con NMF es obtener esas features. Se puede pensar en las t columnas de la matriz W como cada uno de los t clusters de usuarios que contienen valores para cada una de las f categorías. Cuanto más alto sea el valor de wij la categoría i tendrá más importancia en el cluster j. De forma equivalente, cada columna de la matriz H representa el peso que tiene cada cluster para cada usuario. Siguiendo la explicación anterior, en la matriz H tenemos la información de a qué cluster pertenecen los usuarios. Solo tenemos que quedarnos con el cluster que tenga más peso para cada usuario: ![]() Es decir, el usuario j pertenece al cluster k que maximice la expresión anterior. Los centroides de cada cluster se corresponden con las columnas de W. Para más información sobre este algoritmo, puedes consultar el siguiente artículo. Tras aplicar el algoritmo a nuestro dataset, obtenemos los siguientes resultados:
Es decir, el usuario j pertenece al cluster k que maximice la expresión anterior. Los centroides de cada cluster se corresponden con las columnas de W. Para más información sobre este algoritmo, puedes consultar el siguiente artículo. Tras aplicar el algoritmo a nuestro dataset, obtenemos los siguientes resultados: 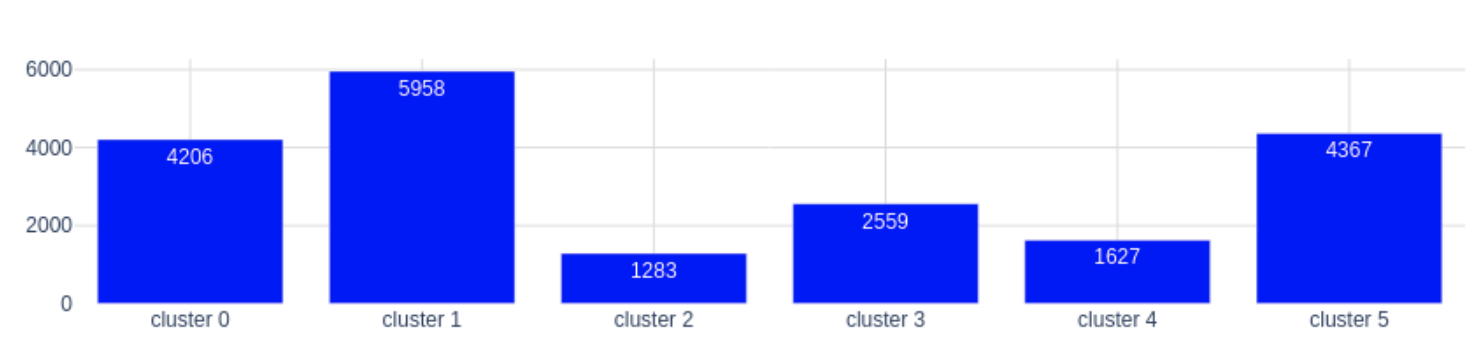
 Como vemos, los tamaños de los clusters son más uniformes y todos los clusters tienen un comportamiento asociado en cuanto a las categorías que compran, aunque hayan comprado poco. Con este resultado podríamos describir a nuestros clusters como:
Como vemos, los tamaños de los clusters son más uniformes y todos los clusters tienen un comportamiento asociado en cuanto a las categorías que compran, aunque hayan comprado poco. Con este resultado podríamos describir a nuestros clusters como:
- Cluster 0: compran en las categorías 2, 9, 12, 17 y 19, pero con poca intensidad.
- Cluster 1: también con poca intensidad pero sobre todo las categorías 13, 1 y 2.
- Cluster 2: en este cluster se encuentran los usuarios que compran con más intensidad y sobre todo las categorías 28, 27, 13, 18, 8 y 29.
- Cluster 3: compran en las categorías 19, 4 y 12.
- Cluster 4: compran en las categorías 13, 27, 8 y 11.
- Cluster 5: compran sobre todo en las categorías 11 y 9 aunque con poca intensidad.
En conclusión, aunque k-means puede funcionar bien en una gran cantidad de problemas, hay que realizar un estudio previo y entender bien de dónde viene y cómo calculamos nuestro dataset. Este análisis puede darnos grandes pistas sobre qué algoritmo es el más apropiado para realizar una buena segmentación. Aparte de esto, no hay que perder el punto de vista de negocio que va a ser el que finalmente nos haga afinar el algoritmo que elijamos para que los grupos sean lo más activables posible. Si te ha gustado este artículo y quieres saber más sobre K-means aplicado a tu negocio, escríbenos a info@makingscience.com






 Configuración de cookies
Configuración de cookies